La double gouttière cycloïdale

La double gouttière cycloïdale est formée de deux canaux identiques juxtaposés ayant la forme d'une demi-cycloïde, une cycloïde étant la courbe décrite par un point d'un cercle qui roule sur une droite. Si on lance simultanément deux billes à des niveaux différents dans ces deux gouttières, elles arrivent en même temps à l' extrémité de la partie incurvée. La durée de la descente d'une bille, dans ce dispositif, ne dépend donc pas de la longueur du trajet (si le trajet est plus long, la bille va plus vite au début) ...  On dit que la cycloïde est une courbe tautochrone pour le mouvement d'un point pesant. 
Si l' on attache une des billes à un fil pour constituer un pendule, tout en obligeant son centre à décrire une cycloïde, on montre que la période, c'est à dire la durée d'oscillation, ne dépend pas de son amplitude : C'est la propriété dite de l'isochronisme des  oscillations.
La recherche d'un pendule isochrone quelle que soit son amplitude a été entreprise dès 1659 par Christian Huygens en vue de régulariser les horloges marines, indispensables pour déterminer correctement la longitude : la terre faisant un tour complet, soit 360°, en 24 heures, un point de la surface terrestre va parcourir 15° de longitude en une heure ; il suffit donc, en principe, de connaître la différence entre l'heure de référence sur le méridien de départ et l'heure locale pour connaître la longitude à un instant et un lieu donnés, d'où la nécessité d'un bon garde-temps pour avoir à tout moment, à bord d'un navire, l'heure du méridien du point de départ. Alors que les horloges à folio pouvaient varier d'au moins une demi-heure par jour avant Huygens, la pendule à balancier de ce dernier améliore beaucoup la précision. 

Mais Christian Huygens voulait trouver un pendule parfaitement isochrone quelle que soit son amplitude. Il établit d'abord la propriété spécifique de la cycloïde : c'est la courbe tautochrone pour le mouvement d'un point pesant. La courbe tautochrone est la courbe plane qu'un point pesant doit parcourir, sans frottement et sans vitesse initiale, pendant une durée indépendante de la longueur du trajet.  Cette propriété peut se vérifier facilement à l'aide de la double gouttière cycloïdale. 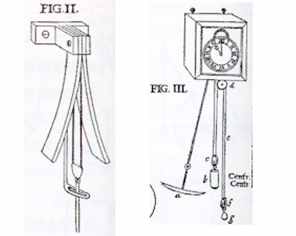Dans son œuvre maîtresse "l'Horloge oscillante", Huygens décrit en 1673 une horloge réalisant l'isochronisme des oscillations pour toutes les amplitudes : le pendule s'y trouve guidé par deux lames métalliques de telle façon que son extrémité décrive non pas un arc de cercle, mais un arc de cycloïde.

Il faudra pourtant attendre un siècle pour que cette horloge, qui semblait peu pratique à utiliser en mer, soit remplacée par des garde-temps ne variant que de quelques secondes par jour, tels que la montre marine de l'anglais John Harrisson, celles de l'horloger d'origine suisse Ferdinand Bertoud mais aussi, à partir de 1769 , par celle du tourangeau Pierre Le Roy, qui est considéré comme le véritable père du chronomètre.

Ajoutons que les calculs nécessaires à la résolution du problème de la  cycloïde courbe tautochrone furent parmi ceux qui ont nécessité une véritable révolution dans l'histoire des mathématiques : la création du calcul différentiel et intégral au 17^ème siècle. (voir l'article de  Jacques Dubois BUP n°737 page 1251 :
Chute d'une bille le long d'une gouttière cycloïdale.Tautochrone et bratistochrone. Propriétés et historique.