Application de la troisième de Kepler
L'observation des satellites de Jupiter, initiée par Galilée en 1610, permet d'obtenir des informations sur la planète géante.
Question
Donner la relation mathématique liant le carré de la période T et le cube du rayon orbital R d'un satellite de Jupiter.
Question
Utiliser cette relation pour en déduire une valeur moyenne de la masse de Jupiter.
période de révolution (j) | distance moyenne à Jupiter (km) | |
Io | 1,77 | 4,20.105 |
Europe | 3,55 | 6,70.105 |
Ganymède | 7,16 | 1,07.106 |
Callisto | 16,7 | 1,88.106 |
Les résultats donnent, en moyenne, MJ = 1,89.1027 kg.
période de révolution (j) | distance moyenne à Jupiter (km) | 4 pi^2 r^3 / GT^2 (kg) | |
Io | 1,77 | 4,20.105 | 1,87.1027 |
Europe | 3,55 | 6,70.105 | 1,89.1027 |
Ganymède | 7,16 | 1,07.106 | 1,89.1027 |
Callisto | 16,7 | 1,88.106 | 1,89.1027 |
Question
Comparer cette masse à celle de la Terre MT = 6.1024 kg ou du Soleil MS = 2.1030 kg.
La planète Jupiter est plus de 300 fois plus massive que la Terre, mais plus de 1 000 fois moins que le Soleil.
Question
Calculer la masse volumique de Jupiter et la comparer à celle des planètes dites internes (comme la Terre), de l'ordre de 5 à 6 gramme par centimètre-cube. Conclure quant à la nature de la planète Jupiter.
Rappel : le diamètre de Jupiter est de l'ordre de 140 000 km.
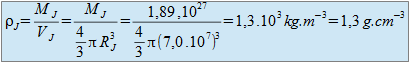
La masse volumique moyenne de Jupiter est cinq fois plus faible que celle d'une planète tellurique : il s'agit d'une planète gazeuse.





