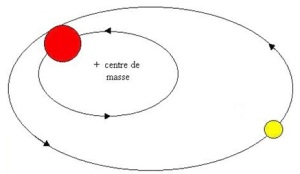
3 - Détermination de la masse du compagnon
Cadre d'étude
La masse d'une planète tellurique, comme la Terre MT = 6 .1024 kg, est près de 1 000 fois plus faible que celle d'une planète gazeuse, comme Jupiter MJ = 2.1027 kg. L'étoile E (masse M) a un astre compagnon C de masse m ; on notera O le centre de masse de ce système binaire. R est la distance de O à E et r la distance de O à C. On notera V la vitesse linéaire de rotation de l'étoile E de masse M et v la vitesse linéaire de rotation de l'astre compagnon de masse m dans le repère barycentrique. Pour simplifier, on se placera dans l'hypothèse d'orbites circulaires. |
Question
Appliquer la deuxième loi de Newton au compagnon dans le référentiel du centre de masse.
Le PFD appliqué au compagnon dans le référentiel du centre de masse s'écrit
![]()
Question
Donner l'expression de la vitesse linéaire v de rotation du compagnon dans le référentiel barycentrique en fonction de r et de la période du système binaire, T.
La vitesse linéaire de rotation du compagnon dans le référentiel barycentrique s'écrivant
![]()
où T est la période du système binaire.
Question
En insérant l'expression précédente dans celle du PFD, montrer que l'on peut écrire (équation E1)
![]()
En insérant l'expression de la vitesse dans la relation issue du PFD,
![]()
soit
![]()
Question
Exprimer R en fonction de Vrad, R et i. Insérer cette expression dans (E1).
Comme ![]() et
et ![]()
![]()
Question
Calculer R puis r à l'aide des données suivantes :
G = 6.67. 10–11 N.m2.kg–2
Vrad = 23,1 km.s–1
T = 10,34 jours ≈ 9,0.105 s
M = 1,05 Msolaire = 1,05 x 2,0.1030 = 2,1.1030 kg
sin i = 1 (par défaut), calculer R puis r.
![]()
r = 0,275 x R = 1,2.1010 m
Question
Utiliser l'égalité des accélérations centripètes de l'étoile et de son compagnon pour établir que
![]()
L'égalité des accélérations centripètes fournit la relation
![]()
d'où l'on extrait
![]()
Question
En utilisant l'expression des vitesses v et V en fonction des paramètres orbitaux, en déduire l'expression de m en fonction de r, R et M.
En utilisant les expressions de v et V en fonction de r, R et T, il vient
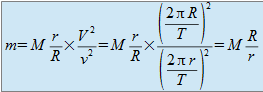
Question
Calculer m. Conclure quant à la taille et à la luminosité probable du compagnon.
m = 0,275 M = 5,8.1029 kg
Le compagnon C de l'étoile E est donc une étoile naine, dont la faible masse semble indiquer qu'elle n'émet pratiquement pas dans le visible !
Remarque : le fait de prendre sin i = 1 donne R par défaut. Si sin i diminue, R augmente, r diminue et donc m augmente. Sin i = 1 donne donc la masse de m par défaut.